Supervised learning and decoding with manifold GPLVMs
Kristopher T. Jensen (February, 2022); ktj21@cam.ac.uk
In this short example notebook, we fit mGPLVM as a supervised learning model (based on Jensen, Kao, Tripodi & Hennequin, NeurIPS 2020).
The general specification of mGPLVM is a latent variable model where the objective is to maximize the marginal likelihood:
where \(p(Y|Z)\) is a Gaussian processes, \(Y \in \mathbb{R}^{N \times T}\) are neural recordings, and \(Z \in T^1\) are some latent variables on a circle (note that everything readily generalizes to higher-dimensional Euclidean and non-Euclidean manifolds).
\[\theta^* = \text{argmax}_\theta \left [ \log p_{\theta}(Y_{train}|Z_{train}) \right ].\]
\[p(Z^*|Y^*, \{Y_{train}, Z_{train}\}) \propto p_{\theta}(Y^* | Z^*, \{Y_{train}, Z_{train}\}) p(Z^*),\]where \(p_{\theta}(Y^* | Z^*, \{Y_{train}, Z_{train}\})\) is given by the standard predictive GP equations. This is of course difficult, and we resort to variational inference using the mGPLVM machinery, but now with frozen generative parameters \(\theta^*\).
See Jensen et al. (2020) for further details about the generative model and inference procedure. Further developments on auto-regressive priors and non-Gaussian noise models were presented at Cosyne 2021 but have not been published.
We start by installing the mGPLVM implementation used in Jensen et al. This is freely available, but the codebase is still under active development with ongoing work on various latent variable models (here we use the ‘bGPFA’ branch which is most up-to-date).
We proceed to load a few packages and set our random seed.
[1]:
#@title Load packages
import time
tic = time.time()
import torch
import mgplvm as mgp
import numpy as np
import matplotlib.pyplot as plt
import pickle
from sklearn.decomposition import FactorAnalysis
from sklearn.linear_model import LinearRegression, Ridge, RidgeCV
from scipy.interpolate import CubicSpline
from scipy.ndimage import gaussian_filter1d
from scipy.stats import binned_statistic, pearsonr, ttest_1samp
plt.rcParams['font.size'] = 20
plt.rcParams['axes.spines.right'] = False
plt.rcParams['axes.spines.top'] = False
device = mgp.utils.get_device() # use GPU if available, otherwise CPU
loading
[2]:
seed = 0 #set the seed
np.random.seed(seed)
torch.manual_seed(seed)
[2]:
<torch._C.Generator at 0x7f2b500eb5b0>
[3]:
#@title Define plot functions
def plot_activity_heatmap(Y):
### plot the activity of our neurons ###
plt.figure(figsize = (12, 6))
plt.imshow(Y[0, ...], cmap = 'Greys', aspect = 'auto', vmin = np.quantile(Y, 0.01), vmax = np.quantile(Y, 0.99))
plt.xlabel('time')
plt.ylabel('neuron')
plt.title('Raw activity', fontsize = 25)
plt.xticks([])
plt.yticks([])
plt.show()
def plot_tuning_curves(fit_thetas, ys_noise, plot_thetas, ys, ys_lin, ys_bins, ys_gp, xs_bins):
plt.figure(figsize = (5,3.0))
plt.scatter(fit_thetas, ys_noise, color = "k", alpha = 0.2)
plt.plot(plot_thetas, ys, 'k-')
plt.plot(plot_thetas, ys_lin, 'b-')
plt.plot(xs_bins, ys_bins, 'g-')
plt.plot(plot_thetas, ys_gp, 'm-')
plt.legend(['true', 'linear', 'binned', 'GP'], frameon = False, ncol = 2, loc = 'upper center', bbox_to_anchor = [0.5, 1.4])
plt.xlim(-np.pi, np.pi)
plt.xlabel('theta')
plt.ylabel('activity')
plt.yticks([])
plt.xticks([-np.pi, 0, np.pi], [r'$-\pi$', r'$0$', r'$\pi$'])
plt.show()
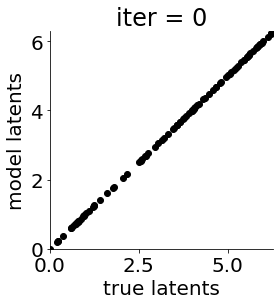
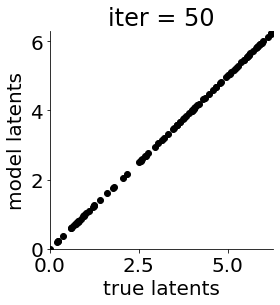
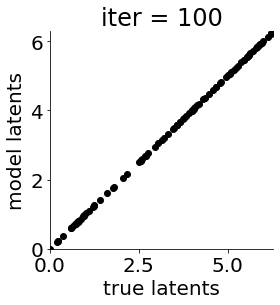
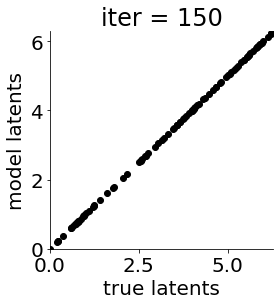
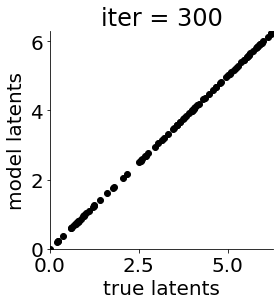
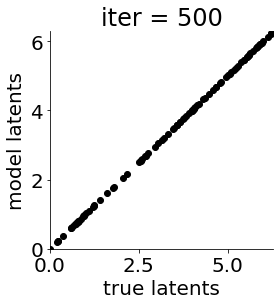
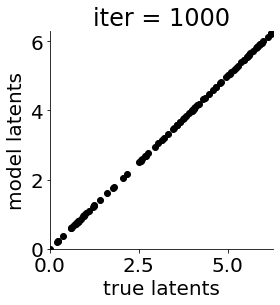
def cb(mod, i, loss):
"""here we construct an (optional) function that helps us keep track of the training"""
if i in [0, 50, 100, 150, 300, 500, 1000, 1500, 1999]: #iterations to plot
X = mod.lat_dist.prms[0].detach().cpu().numpy()[0, ...]
X = X % (2*np.pi)
plt.figure(figsize = (4,4))
plt.xlim(0, 2*np.pi); plt.ylim(0, 2*np.pi)
plt.xlabel("true latents"); plt.ylabel("model latents")
plt.scatter(thetas_plot, X[:, 0], color = 'k')
plt.title('iter = '+str(i))
plt.show()
print(mod.lat_dist.msg(Y, None, None) + mod.svgp.msg + mod.lprior.msg, loss/n_ts1)
def plot_final_thetas(thetas2, thetas2_lin, thetas2_mgplvm):
plt.figure()
plt.scatter(thetas2, thetas2_lin, color = "b")
plt.scatter(thetas2, thetas2_mgplvm, color = "k")
plt.legend(['linear', 'mgplvm'], frameon = False, ncol = 2, loc = 'upper center', bbox_to_anchor = (0.5, 1.25))
plt.xlabel('true theta')
plt.ylabel('predicted theta')
plt.show()
def plot_final_errors(errs_lin, errs_mgplvm, bins):
plt.figure()
plt.hist(errs_lin, bins = bins, color = 'b', alpha = 0.2)
plt.hist(errs_mgplvm, bins = bins, color = 'k', alpha = 0.2)
plt.axvline(np.mean(errs_lin), color = 'b', lw = 3)
plt.axvline(np.mean(errs_mgplvm), color = 'k', lw = 3)
plt.xlabel('error')
plt.ylabel('frequency')
plt.legend(['linear', 'mgplvm'], frameon = False)
plt.show()
def plot_uncertainty_estimates(xs, errs_by_uncertainty):
#xs, errs_by_uncertainty = xs**2, errs_by_uncertainty**2 #variances instead of stds
plt.figure(figsize = (5,5))
plt.scatter(xs, errs_by_uncertainty, color = "k")
plt.plot([xs[0], xs[-1]], [xs[0], xs[-1]], "k-")
plt.xlabel("uncertainty")
plt.ylabel("RMSE")
plt.xticks([0.15, 0.20, 0.25])
plt.yticks([0.15, 0.20, 0.25])
plt.show()
In order to validate the method, we generate synthetic data from 40 neurons and 100 time points, assuming ‘Gaussian bump’-like tuning curves and Gaussian noise. We use this fairly sparse dataset to illustrate the data efficiency of this approach, but it would of course also work with more data. We also note that the codebase readily allows for Poisson or negative binomial noise models.
[4]:
### generate some synthetic data ###
n_ts = 600 #total time points
n_ts1 = 100 #training time points
n_neurons = 40 #number of neurons
thetas = np.zeros(n_ts) #generate a sequence of angles as an autoregressive process
for i in range(1, n_ts):
thetas[i] = (thetas[i-1] + np.random.normal()) % (2*np.pi)
prefs = np.sort(np.random.uniform(0, 2*np.pi, n_neurons)) #preferred orientations
deltas = prefs[:, None] - thetas[None, :] #difference from head direction
gs = np.random.uniform(0.5, 1.5, n_neurons) #scale variables
kappas = np.random.uniform(2, 4, n_neurons) #concentration parameters
#generate activity
Y = gs[:, None] * np.exp( kappas[:, None]*( np.cos(deltas) - 1 ) ) + np.random.normal(0, 0.5, (n_neurons, n_ts))
Y = Y[None, ...]
#split into train and test
Y1 = Y[:, :, :n_ts1] #train
thetas1 = thetas[:n_ts1]
Y2 = Y[:, :, n_ts1:] #test
### plot the training data we just generated ###
plot_activity_heatmap(Y1)

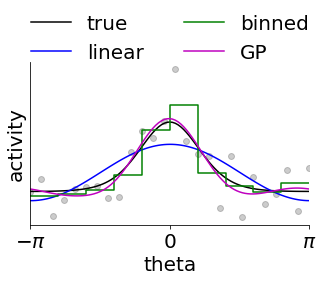
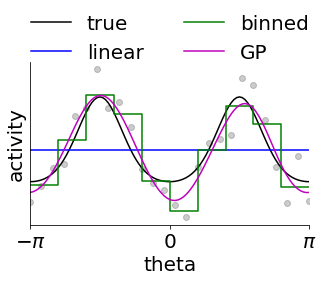
In this next code snippet, we consider why fitting this GPLVM-based model might be a good idea. To do this, we consider an example neuron from above and try to approximate its tuning using three different approached.
The first is by assuming linearity in \([\cos\theta, \sin \theta]\) which is what many linear decoders of angles do. However, this enforces a sinusoidal tuning curve which does not fit the data well.
The second is to bin the data and construct an empirical tuning curve as the average activity in each bin (note that this corresponds to a Gaussian noise model, and we could equally well use non-Gaussian noise models). However, this requires us to specify a priori what the resolution is, and it leads to non-intuitive discontinuities. This is the approach taken by many standard Bayesian decoders. In fact, this is equivalent to fitting a Gaussian Process with a kernel that is constant within each bin and discontinuous between bins.
Alternatively, we can posit that the expected similarity of neural activity is not discrete but rather a function of distance on the circle. We do this by fitting a Gaussian process to the data with a kernel that ensures smoothness/continuity on the circle. Importantly, the length scale can now be learned directly from the data and there are no discontinuities. This is particularly important in the limited-data regime, and we see that this model fits the data better.
[5]:
plot_thetas = np.linspace(-np.pi, np.pi, 101) #values to use for plotting
inds = np.arange(0, len(plot_thetas), 4) #only record a subset of angles
for example in range(2):
if example == 0: #single neuron
ys = 1.4 * np.exp( 2.3*( np.cos(plot_thetas) - 1 ) ) #tuning curve
ell = 1/np.sqrt(2.3)
else:
ys1 = 1.4 * np.exp( 4*( np.cos(plot_thetas + 0.5*np.pi) - 1 ) ) #tuning curve
ys2 = 1.4 * np.exp( 4*( np.cos(plot_thetas - 0.5*np.pi) - 1 ) ) #tuning curve
ys = ys1+ys2
ell = 1/np.sqrt(4)
ys_noise = (ys + np.random.normal(0, 0.3, len(plot_thetas)))[inds] #noisy data
fit_thetas = plot_thetas[inds] #supervised angles for our noisy data
### fit the linear model ###
cs_plot = np.array([np.cos(plot_thetas), np.sin(plot_thetas)]).T #cos/sin
cs_fit = cs_plot[inds, :] #for our noisy data data
clf_single = RidgeCV(alphas=10**np.linspace(-5,5,51)).fit(cs_fit, ys_noise[:, None]) #crossvalidated ridge regression
ys_lin = clf_single.predict(cs_plot) #fitted tuning curve
### binned decoder ###
bins = np.linspace(-np.pi, np.pi, 11) #assume 11 bins for now
ys_bins = binned_statistic(fit_thetas, ys_noise, bins = bins)[0] #activity in each bin
ys_bins = np.repeat(ys_bins, 2) #expand for plotting
xs_bins = np.repeat(bins, 2)[1:-1] #expand for plotting
### fit out GP-based model ###
def K(x1, x2, ell = 0.75, sig = 0.3):
'''for illustration purposes, we pick some reasonable parameters but these could be learned from data'''
Kmat = np.exp( (np.cos(x1[:, None] - x2[None, :]) - 1) / (2*ell**2) )
if (sig > 0) and (x1.shape == x2.shape): Kmat += sig*np.eye(len(fit_thetas))
return Kmat
#GP inference
ys_gp = K(plot_thetas, fit_thetas, sig = 0, ell = ell) @ np.linalg.inv(K(fit_thetas, fit_thetas, ell = ell)) @ ys_noise
ys_gp = ys_gp.flatten()
### plot result ###
plot_tuning_curves(fit_thetas, ys_noise, plot_thetas, ys, ys_lin, ys_bins, ys_gp, xs_bins)
Having gained some intuition for the benefits of Gaussian process-based models, we are ready to construct our full mGPLVM for decoding. In the following code snippet, we set a couple of model parameters relating to the optimization process and initialization. Most of the initialization is done directly from the data, but it can be useful to include if we have prior knowledge about e.g. the timescale of the behavior we care about.
[6]:
### set some parameters for fitting ###
max_steps = 1001 # number of training iterations
n_mc = 1 # number of monte carlo samples per iteration (since the latents are a delta function, we only need 1)
print_every = 100 # how often we print training progress
d_latent = 1 # specify the dimensionality of the space
n_z = 10 #number of inducing points; performance increases with more inducing points
Having specified our parameters, we can construct the mGPLVM model. In this particular library, we need to separately specify (i) the noise model, (ii) the latent manifold (see Jensen et al. 2020 for various manifolds), (iii) the prior and variational distribution, and (iv) the GP kernel.
For this dataset we use a Gaussian noise model, but we can easily swap in a count-based model. Note how we set the latent distribution to be centered at the ground truth thetas and have a very small standard deviation (1e-5; effectively a delta function).
[7]:
### construct the actual model ###
n_trials, n_neurons, n_ts1 = Y1.shape
data1 = torch.Tensor(Y1).to(device)
manif = mgp.manifolds.Torus(n_ts1, d_latent) # our latent variables live on a ring (see Jensen et al. 2020 for alternatives)
likelihood = mgp.likelihoods.Gaussian(n_neurons, Y = Y1, d = d_latent) #Gaussian noise
mu = thetas1[None, :, None] #ground truth thetas for training
lat_dist = mgp.rdist.ReLie(manif, n_ts1, n_trials, sigma = 1e-5, diagonal = True, mu = mu) #latent distribution
lprior = mgp.lpriors.Uniform(manif) #note that we could also learn the generative parameters of a parametric prior
kernel = mgp.kernels.QuadExp(n_neurons, manif.distance, Y = Y1, ell = np.ones(n_neurons)*1, scale = 0.7*np.ones(n_neurons)) #squared exponential kernel
z = manif.inducing_points(n_neurons, n_z) #inducing points
mod = mgp.models.SvgpLvm(n_neurons, n_ts1, n_trials, z, kernel, likelihood, lat_dist, lprior).to(device) #construct model
We are now ready to actually learn the generative parameters!
[8]:
t0 = time.time()
thetas_plot = thetas1
#note that the 'mask_Ts' function is a mask applied to the gradients for the variational distribution
#by setting these gradients to zero, we are imposing the ground truth latents and doing supervised training
train_params = mgp.crossval.training_params(max_steps = max_steps, n_mc = n_mc, lrate = 5e-2, callback = cb, burnin = 50, mask_Ts = (lambda x: x*0))
print('fitting', n_neurons, 'neurons and', n_ts1, 'time bins for', max_steps, 'iterations')
mod_train = mgp.crossval.train_model(mod, data1, train_params)
fitting 40 neurons and 100 time bins for 1001 iterations
iter 0 | elbo -3.913 | kl 0.298 | loss 3.913 | |mu| 3.944 | sig 0.000 | scale 0.700 | ell 1.000 | lik_sig 0.836 |
|mu| 3.944 | sig 0.000 | scale 0.700 | ell 1.000 | lik_sig 0.836 | 156.5077596119108
iter 50 | elbo -1.056 | kl 0.297 | loss 1.244 | |mu| 3.944 | sig 0.000 | scale 0.664 | ell 1.160 | lik_sig 0.834 |
|mu| 3.944 | sig 0.000 | scale 0.664 | ell 1.160 | lik_sig 0.834 | 49.74203195518805
iter 100 | elbo -0.843 | kl 0.300 | loss 1.103 | |mu| 3.944 | sig 0.000 | scale 0.630 | ell 1.303 | lik_sig 0.531 |
|mu| 3.944 | sig 0.000 | scale 0.630 | ell 1.303 | lik_sig 0.531 | 44.10655420896538
iter 150 | elbo -0.804 | kl 0.298 | loss 1.087 | |mu| 3.944 | sig 0.000 | scale 0.596 | ell 1.366 | lik_sig 0.511 |
|mu| 3.944 | sig 0.000 | scale 0.596 | ell 1.366 | lik_sig 0.511 | 43.48937458010431
iter 200 | elbo -0.794 | kl 0.296 | loss 1.085 | |mu| 3.944 | sig 0.000 | scale 0.575 | ell 1.368 | lik_sig 0.504 |
iter 250 | elbo -0.790 | kl 0.297 | loss 1.084 | |mu| 3.944 | sig 0.000 | scale 0.560 | ell 1.354 | lik_sig 0.501 |
iter 300 | elbo -0.787 | kl 0.301 | loss 1.087 | |mu| 3.944 | sig 0.000 | scale 0.548 | ell 1.339 | lik_sig 0.499 |
|mu| 3.944 | sig 0.000 | scale 0.548 | ell 1.339 | lik_sig 0.499 | 43.49780433490198
iter 350 | elbo -0.786 | kl 0.300 | loss 1.086 | |mu| 3.944 | sig 0.000 | scale 0.539 | ell 1.324 | lik_sig 0.498 |
iter 400 | elbo -0.785 | kl 0.301 | loss 1.086 | |mu| 3.944 | sig 0.000 | scale 0.531 | ell 1.310 | lik_sig 0.497 |
iter 450 | elbo -0.785 | kl 0.300 | loss 1.084 | |mu| 3.944 | sig 0.000 | scale 0.524 | ell 1.298 | lik_sig 0.497 |
iter 500 | elbo -0.784 | kl 0.298 | loss 1.082 | |mu| 3.944 | sig 0.000 | scale 0.517 | ell 1.287 | lik_sig 0.496 |
|mu| 3.944 | sig 0.000 | scale 0.517 | ell 1.287 | lik_sig 0.496 | 43.275065719273954
iter 550 | elbo -0.784 | kl 0.295 | loss 1.079 | |mu| 3.944 | sig 0.000 | scale 0.511 | ell 1.277 | lik_sig 0.496 |
iter 600 | elbo -0.784 | kl 0.302 | loss 1.085 | |mu| 3.944 | sig 0.000 | scale 0.506 | ell 1.267 | lik_sig 0.496 |
iter 650 | elbo -0.783 | kl 0.300 | loss 1.083 | |mu| 3.944 | sig 0.000 | scale 0.501 | ell 1.258 | lik_sig 0.496 |
iter 700 | elbo -0.783 | kl 0.296 | loss 1.079 | |mu| 3.944 | sig 0.000 | scale 0.496 | ell 1.248 | lik_sig 0.495 |
iter 750 | elbo -0.783 | kl 0.297 | loss 1.080 | |mu| 3.944 | sig 0.000 | scale 0.492 | ell 1.237 | lik_sig 0.495 |
iter 800 | elbo -0.783 | kl 0.300 | loss 1.083 | |mu| 3.944 | sig 0.000 | scale 0.488 | ell 1.225 | lik_sig 0.495 |
iter 850 | elbo -0.783 | kl 0.297 | loss 1.080 | |mu| 3.944 | sig 0.000 | scale 0.484 | ell 1.212 | lik_sig 0.495 |
iter 900 | elbo -0.783 | kl 0.298 | loss 1.081 | |mu| 3.944 | sig 0.000 | scale 0.480 | ell 1.201 | lik_sig 0.495 |
iter 950 | elbo -0.782 | kl 0.298 | loss 1.080 | |mu| 3.944 | sig 0.000 | scale 0.476 | ell 1.189 | lik_sig 0.495 |
iter 1000 | elbo -0.782 | kl 0.301 | loss 1.083 | |mu| 3.944 | sig 0.000 | scale 0.473 | ell 1.178 | lik_sig 0.495 |
|mu| 3.944 | sig 0.000 | scale 0.473 | ell 1.178 | lik_sig 0.495 | 43.314183433002384
We proceed to train a simple linear model which we will use as a baseline. We also use the predictions of the linear model for initialization.
[9]:
## first fit a linear model (we will use this for initialization and comparison) ##
Y2 = Y[..., n_ts1:] #test data
thetas2 = thetas[n_ts1:] #true test angles
Z1 = np.array([np.cos(thetas1), np.sin(thetas1)]).T #true training cos/sin
Z2 = np.array([np.cos(thetas2), np.sin(thetas2)]).T #true test cos/sin
print(Y1.shape, Z1.shape)
alphas = 10**(np.linspace(-4, 4, 51)) #possible regularization strengths
clf = RidgeCV(alphas=alphas).fit(Y1[0, ...].T, Z1) #crossvalidated ridge regression
Z2_pred = clf.predict(Y2[0, ...].T) #predict test data
Z2_pred = Z2_pred / np.sqrt(np.sum(Z2_pred**2, axis = 1, keepdims = True)) #normalize
thetas2_lin = (np.sign(Z2_pred[:, 1]) * np.arccos(Z2_pred[:, 0])) % (2*np.pi) #predicted angles
(1, 40, 100) (100, 2)
We’re now ready for the prediction step. Here we copy over all parameters from our previous model apart from the variational distribution which we define anew.
[10]:
### now we want to do decoding ###
_, _, n_ts2 = Y2.shape
manif2 = mgp.manifolds.Torus(n_ts2, d_latent) # latent manifold is still a circle
#compute displacements to use a better prior
displacements = thetas1[1:] - thetas1[:-1]
displacements[displacements < -np.pi] += 2*np.pi
displacements[displacements > np.pi] -= 2*np.pi
print(np.std(displacements)) #matches generative process
mu2 = thetas2_lin[None, :, None] #initialize from linear prediction
#lprior2 = mgp.lpriors.Uniform(manif2) #uniform prior
#let's assume some degree of continuity in the data
lprior2 = mgp.lpriors.Brownian(manif2, fixed_brownian_c = True, fixed_brownian_eta = True,
brownian_eta = torch.ones(d_latent) * np.var(displacements))
lat_dist2 = mgp.rdist.ReLie(manif2, n_ts2, n_trials, sigma = 0.5, diagonal = True, mu = mu2) #variational distribution
1.0123699125250345
[11]:
#@title Construct inference model
data2 = torch.Tensor(Y2).to(device) #put data on device
mod2 = mgp.models.SvgpLvm(n_neurons, n_ts2, n_trials, z.cpu(), kernel.cpu(), likelihood.cpu(), lat_dist2, lprior2).to(device) #use old generative model and new variational distribution
for p in mod2.parameters(): #no gradients for generative parameters
p.requires_grad = False
for p in mod2.lat_dist.parameters(): #only inference
p.requires_grad = True
#copy over tuning curves (this summarizes p(Y*|Z*, {Y, Z}) from the training data in the SVGP framework)
mod2.svgp.q_mu[...] = mod.svgp.q_mu[...].detach()
mod2.svgp.q_sqrt[...] = mod.svgp.q_sqrt[...].detach()
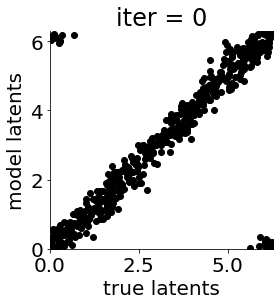
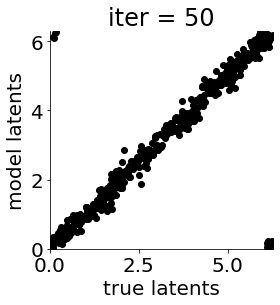
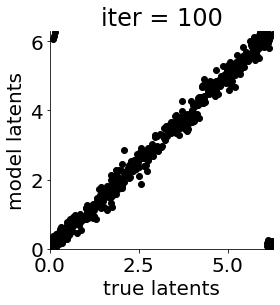
Finally we infer our new latents using the mGPLVM machinery!
[12]:
t0 = time.time()
thetas_plot = thetas2
# helper function to specify training parameters. We now do not mask the gradients.
train_params2 = mgp.crossval.training_params(max_steps = max_steps, n_mc = 20, lrate = 2e-2, print_every = 10, callback = cb, burnin = 1, mask_Ts = (lambda x: x*1))
print('fitting', n_neurons, 'neurons and', n_ts2, 'time bins for', max_steps, 'iterations')
mod_train2 = mgp.crossval.train_model(mod2, data2, train_params2) #inference!
fitting 40 neurons and 500 time bins for 1001 iterations
iter 0 | elbo -0.896 | kl 0.024 | loss 0.896 | |mu| 3.670 | sig 0.500 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
|mu| 3.670 | sig 0.500 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 | 179.19064879098534
iter 10 | elbo -0.871 | kl 0.025 | loss 0.896 | |mu| 3.669 | sig 0.445 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 20 | elbo -0.851 | kl 0.026 | loss 0.877 | |mu| 3.673 | sig 0.384 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 30 | elbo -0.839 | kl 0.028 | loss 0.867 | |mu| 3.679 | sig 0.335 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 40 | elbo -0.828 | kl 0.031 | loss 0.859 | |mu| 3.683 | sig 0.295 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 50 | elbo -0.820 | kl 0.034 | loss 0.854 | |mu| 3.686 | sig 0.265 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
|mu| 3.686 | sig 0.265 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 | 170.80025111998782
iter 60 | elbo -0.816 | kl 0.035 | loss 0.851 | |mu| 3.685 | sig 0.242 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 70 | elbo -0.812 | kl 0.037 | loss 0.849 | |mu| 3.684 | sig 0.225 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 80 | elbo -0.810 | kl 0.039 | loss 0.848 | |mu| 3.684 | sig 0.212 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 90 | elbo -0.807 | kl 0.040 | loss 0.847 | |mu| 3.687 | sig 0.202 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 100 | elbo -0.806 | kl 0.041 | loss 0.847 | |mu| 3.686 | sig 0.193 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
|mu| 3.686 | sig 0.193 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 | 169.3359999584735
iter 110 | elbo -0.804 | kl 0.042 | loss 0.846 | |mu| 3.687 | sig 0.186 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 120 | elbo -0.804 | kl 0.042 | loss 0.846 | |mu| 3.685 | sig 0.181 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 130 | elbo -0.803 | kl 0.043 | loss 0.846 | |mu| 3.685 | sig 0.177 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 140 | elbo -0.803 | kl 0.043 | loss 0.846 | |mu| 3.686 | sig 0.174 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 150 | elbo -0.802 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.171 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
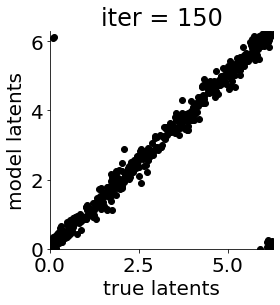
|mu| 3.686 | sig 0.171 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 | 169.16463894396955
iter 160 | elbo -0.802 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.170 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 170 | elbo -0.802 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.168 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 180 | elbo -0.802 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.167 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 190 | elbo -0.802 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.166 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 200 | elbo -0.802 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.164 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 210 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.685 | sig 0.164 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 220 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.164 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 230 | elbo -0.802 | kl 0.044 | loss 0.846 | |mu| 3.688 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 240 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 250 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 260 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 270 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.685 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 280 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.687 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 290 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.687 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 300 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.684 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
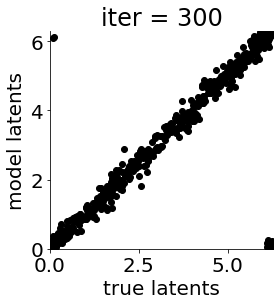
|mu| 3.684 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 | 169.1358956642593
iter 310 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 320 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.685 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 330 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.687 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 340 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.685 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 350 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.686 | sig 0.164 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 360 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.687 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 370 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.685 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 380 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.686 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 390 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.687 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 400 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.687 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 410 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.687 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 420 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 430 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.685 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 440 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 450 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 460 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.688 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 470 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.687 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 480 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.685 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 490 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.687 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 500 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.685 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
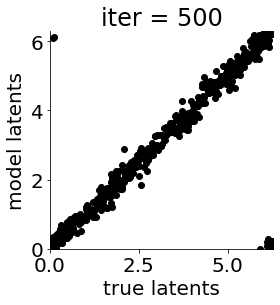
|mu| 3.685 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 | 169.16159645689314
iter 510 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 520 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.687 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 530 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.685 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 540 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.685 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 550 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.686 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 560 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.686 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 570 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.687 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 580 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.685 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 590 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.686 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 600 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 610 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.686 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 620 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.686 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 630 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.687 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 640 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 650 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.686 | sig 0.161 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 660 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.685 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 670 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.685 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 680 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.686 | sig 0.161 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 690 | elbo -0.802 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 700 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.685 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 710 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.687 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 720 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.687 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 730 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.685 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 740 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 750 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.685 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 760 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.686 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 770 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 780 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.687 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 790 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 800 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.687 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 810 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.687 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 820 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 830 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.687 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 840 | elbo -0.802 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 850 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.686 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 860 | elbo -0.802 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 870 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.686 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 880 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.685 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 890 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.687 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 900 | elbo -0.802 | kl 0.044 | loss 0.846 | |mu| 3.687 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 910 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.686 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 920 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.686 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 930 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.687 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 940 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.687 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 950 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.687 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 960 | elbo -0.801 | kl 0.044 | loss 0.846 | |mu| 3.687 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 970 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.687 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 980 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.685 | sig 0.163 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 990 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.685 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
iter 1000 | elbo -0.801 | kl 0.045 | loss 0.846 | |mu| 3.688 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 |
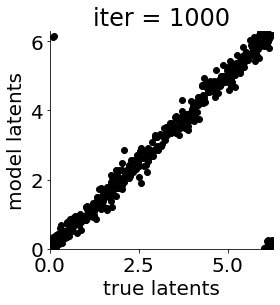
|mu| 3.688 | sig 0.162 | scale 0.473 | ell 1.178 | lik_sig 0.495 | brownian_c 0.000 | brownian_eta 1.025 | 169.15263993430926
We can then compare the performance of the simple linear decoder and our non-linear non-Euclidean mGPLVM-based decoder.
[13]:
#let's do some simple evaluation
#plot inferred vs true angles
thetas2_mgplvm = mod2.lat_dist.prms[0].detach().cpu().numpy()[0, :, 0] % (2*np.pi) #mgplvm prediction
print(thetas2.shape, thetas2_lin.shape, thetas2_mgplvm.shape)
plot_final_thetas(thetas2, thetas2_lin, thetas2_mgplvm)
#compute errors in absolute distance
errs_lin, errs_mgplvm = [np.arccos(np.cos(thetas2 - arr)) for arr in [thetas2_lin, thetas2_mgplvm]]
bins = np.linspace(0, 0.6, 15)
plot_final_errors(errs_lin, errs_mgplvm, bins)
#print some summary statistics
print('average errors:', np.mean(errs_lin), '(linear),', np.mean(errs_mgplvm), '(mgplvm)\n') #print errors
print(ttest_1samp(errs_lin-errs_mgplvm, 0)) #statistical test
(500,) (500,) (500,)
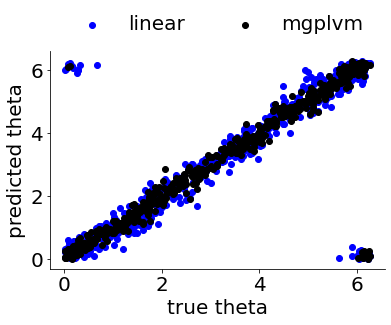
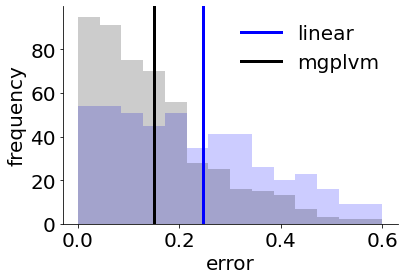
average errors: 0.24719006903707 (linear), 0.1495513829871003 (mgplvm)
Ttest_1sampResult(statistic=11.06075729330881, pvalue=1.3881822209953397e-25)
Finally, we note that the mGPLVM decoder also provides uncertainty estimates in the form of a full distribution over \(p(Z^* | Y^*)\). Here, we shower that these uncertainty estimates are in fact well-calibrated, suggesting that they can be useful for uncertainty-sensitive downstream applications and analyses.
[14]:
## check whether our uncertainty estimates are well-calibrated##
sigmas = mod2.lat_dist.prms[1].detach().cpu().numpy()[0, :, 0, 0] #model uncertainty
print('68.3% ci:', 100*np.mean(errs_mgplvm < sigmas))
print('95.4% ci:', 100*np.mean(errs_mgplvm < 2*sigmas))
### now check whether the empirical std of of the residuals matches the model uncertainty###
bins = np.concatenate([np.sort(sigmas)[::75], [np.inf]]) #construct some bins in which to compute errors
print(np.histogram(sigmas, bins = bins)[0]) #how many observations in each bin
def RMSE(residuals):
'''compute RMSE for a set of residuals'''
return np.sqrt(np.mean(residuals**2))
#compute std of the residuals for each uncertainty bin
errs_by_uncertainty = binned_statistic(sigmas, errs_mgplvm, statistic = RMSE, bins = bins)[0]
#binned x-values taking the average within each bin
xs = binned_statistic(sigmas, sigmas, statistic = RMSE, bins = bins)[0]
### plot RMSE vs uncertainty ###
plot_uncertainty_estimates(xs, errs_by_uncertainty)
print('correlation:', pearsonr(xs, errs_by_uncertainty))
print('total duration:', time.time() - tic)
68.3% ci: 63.800000000000004
95.4% ci: 91.8
[75 75 75 75 75 75 50]
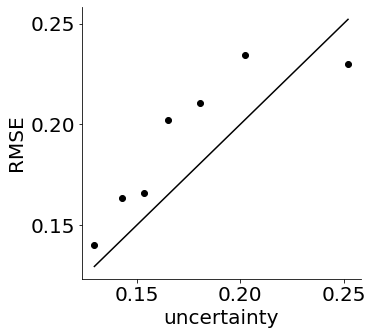
correlation: (0.8755737655495163, 0.009798358756537113)
total duration: 100.79450035095215
##SO(3) For those who have the courage, we now validate this approach on the group of 3D rotations (SO(3)).
[15]:
#@title SO(3) helper functions
def quaternion_multiply(quaternion1, quaternion2):
#this is q1 \times q2
w1, x1, y1, z1 = quaternion1
w2, x2, y2, z2 = quaternion2
return np.array([-x1 * x2 - y1 * y2 - z1 * z2 + w1 * w2,
x1 * w2 + y1 * z2 - z1 * y2 + w1 * x2,
-x1 * z2 + y1 * w2 + z1 * x2 + w1 * y2,
x1 * y2 - y1 * x2 + z1 * w2 + w1 * z2])
def cb_so3(mod, i, loss):
"""here we construct an (optional) function that helps us keep track of the training"""
if i in [0, 50, 100, 150, 250, 350, 500, 750, 1000, 1250, 1500, 1999]: #iterations to plot
print(i, mod.lat_dist.msg(Y, None, None) + mod.svgp.msg + mod.lprior.msg, loss/n_ts1)
We start by generating some data on SO(3) using an autoregressive process. We also construct a set of neurons with preferred firing fields on SO(3).
[16]:
### Try SO(3) ###
### generate some synthetic data ###
tic = time.time()
n_ts = 800 #total time points
n_ts1 = 400 #training time points
n_neurons = 100 #number of neurons
#generate quaternions over time using an autoregressive process
qs_t = np.random.normal(0, 1, (n_ts, 4)) #random points on sphere
qs_t = qs_t / np.sqrt(np.sum(qs_t**2, axis = 1, keepdims = True)) #normalize
for t in range(1, n_ts): #autoregressive process
step = np.random.normal(0, 0.4, 3) #displacement in tangent space
theta = np.sqrt(np.sum(step**2))
v = step / theta
qt = np.concatenate([np.ones(1)*np.cos(theta), np.sin(theta)*v]) #displacement in quaternion space
qs_t[t, :] = quaternion_multiply(qt, qs_t[t-1, :])
#print(qs_t[t, :], np.sum(qs_t[t, :]**2), theta)
qs_t = np.sign(qs_t[:, :1]) * qs_t #consistent sign
#generate preferred orientation for each neuron
qs_n = np.random.normal(0, 1, (n_neurons, 4))
qs_n = qs_n / np.sqrt(np.sum(qs_n**2, axis = 1, keepdims = True))
qs_n = np.sign(qs_n[:, :1]) * qs_n #random quaternions
qs_n = qs_n[np.argsort(qs_n[:, 0]), :] #sort by first element for visualization
deltas = 4*( 1 - (qs_n @ qs_t.T)**2 ) #difference for each neuron/time (x^2 in small angle limit)
dt_dists = 4*( 1 - np.sum(qs_t[:-1, :] * qs_t[1:, :], axis = 1)**2 )
print('consecutive displacements:', np.quantile(dt_dists, [0.1, 0.25, 0.5, 0.75, 0.9]))
print('baseline/random:', np.quantile(deltas.flatten(), [0.1, 0.25, 0.5, 0.75, 0.9]))
consecutive displacements: [0.35885536 0.76547395 1.34929525 2.14503775 2.91410946]
baseline/random: [1.40482737 2.39040575 3.34394689 3.84129081 3.97570362]
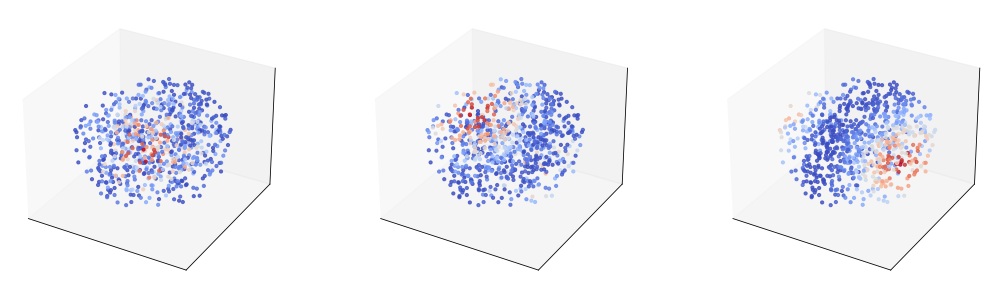
We proceed to generate some synthetic neural activity and visualize it together with a couple of example tuning curves.
[17]:
#generate activity
gs = np.random.uniform(0.5, 1.5, n_neurons) #scale variables
ells = np.random.uniform(1.0, 2, n_neurons) #concentration parameters
F = gs[:, None] * np.exp( - deltas / (2*ells[:, None]**2) )
Y = F + np.random.normal(0, 0.4, (n_neurons, n_ts))
Y = Y[None, ...]
#split into train and test
Y1 = Y[:, :, :n_ts1] #train
thetas1 = qs_t[:n_ts1, :]
Y2 = Y[:, :, n_ts1:] #test
### plot the training data we just generated ###
plot_activity_heatmap(Y1[:, :, np.argsort(qs_t[:n_ts1, 1])])
### also plot some example tuning curves ###
a = qs_t[..., :1]
theta = 2 * np.arccos(a) #magnitude of rotation; ||x|| = theta/2
u = qs_t[..., 1:] / np.sqrt(np.sum(qs_t[..., 1:]**2, axis = -1, keepdims=True))
xs = 0.5 * theta * u
print('\n\ntuning curves:')
from mpl_toolkits import mplot3d
plt.figure(figsize = (15,4.5))
for i in range(3):
ax = plt.subplot(1,3,i+1, projection='3d')
n = np.random.choice(n_neurons)
ax.scatter3D(xs[:, 0], xs[:, 1], xs[:,2], c = F[n, :], cmap = 'coolwarm', alpha = 0.8, s = 10)
ax.set_xticks([]); ax.set_yticks([]); ax.set_zticks([])
plt.tight_layout()
plt.show()

tuning curves:
We not construct our model. In this case, we learn the parameters of the prior directly during model training (note that we could also have done this for the circle; we just defined the prior separately for clarity of exposition).
[18]:
### set some parameters for fitting ###
max_steps = 1501 # number of training iterations
n_mc = 1 # number of monte carlo samples per iteration (since the latents are a delta function, we only need 1)
print_every = 100 # how often we print training progress
d_latent = 3 # specify the dimensionality of the space
n_z = 15 #number of inducing points; performance increases with more inducing points
### construct the actual model ###
n_trials, n_neurons, n_ts1 = Y1.shape
data1 = torch.Tensor(Y1).to(device)
manif = mgp.manifolds.So3(n_ts1, d_latent) # our latent variables live on SO(3) (see Jensen et al. 2020 for alternatives)
likelihood = mgp.likelihoods.Gaussian(n_neurons, Y = Y1, d = d_latent) #Gaussian noise
mu = qs_t[None, :n_ts1, :] #ground truth thetas for training
lat_dist = mgp.rdist.ReLie(manif, n_ts1, n_trials, sigma = 1e-5, diagonal = True, mu = mu) #latent distribution
#learn the prior!
lprior = mgp.lpriors.Brownian(manif, fixed_brownian_c = True, fixed_brownian_eta = False, brownian_eta = torch.ones(d_latent)*0.5**2)
kernel = mgp.kernels.QuadExp(n_neurons, manif.distance, Y = Y1, ell = np.ones(n_neurons)*1.0, scale = 0.7*np.ones(n_neurons)) #squared exponential kernel
z = manif.inducing_points(n_neurons, n_z) #inducing points
mod = mgp.models.SvgpLvm(n_neurons, n_ts1, n_trials, z, kernel, likelihood, lat_dist, lprior).to(device) #construct model
No we’re ready to train the model! This will take a bit longer since we’re using more neurons and time points.
[19]:
t0 = time.time()
train_params = mgp.crossval.training_params(max_steps = max_steps, n_mc = n_mc, lrate = 5e-2, callback = cb_so3, print_every = 27, burnin = 50, mask_Ts = (lambda x: x*0))
print('fitting', n_neurons, 'neurons and', n_ts1, 'time bins for', max_steps, 'iterations')
mod_train = mgp.crossval.train_model(mod, data1, train_params)
fitting 100 neurons and 400 time bins for 1501 iterations
iter 0 | elbo -4.234 | kl 414.281 | loss 4.234 | |mu| 0.500 | sig 0.000 | scale 0.700 | ell 1.000 | lik_sig 0.615 | brownian_c 0.000 | brownian_eta 0.250 |
0 |mu| 0.500 | sig 0.000 | scale 0.700 | ell 1.000 | lik_sig 0.615 | brownian_c 0.000 | brownian_eta 0.250 | 423.4367969499163
iter 27 | elbo -1.188 | kl 414.324 | loss 174.066 | |mu| 0.500 | sig 0.000 | scale 0.678 | ell 0.996 | lik_sig 0.678 | brownian_c 0.000 | brownian_eta 0.147 |
50 |mu| 0.500 | sig 0.000 | scale 0.645 | ell 1.048 | lik_sig 0.713 | brownian_c 0.000 | brownian_eta 0.156 | 26297.472139204503
iter 54 | elbo -1.030 | kl 415.259 | loss 275.269 | |mu| 0.500 | sig 0.000 | scale 0.639 | ell 1.063 | lik_sig 0.713 | brownian_c 0.000 | brownian_eta 0.158 |
iter 81 | elbo -0.915 | kl 414.933 | loss 333.734 | |mu| 0.500 | sig 0.000 | scale 0.594 | ell 1.196 | lik_sig 0.665 | brownian_c 0.000 | brownian_eta 0.161 |
100 |mu| 0.500 | sig 0.000 | scale 0.560 | ell 1.327 | lik_sig 0.589 | brownian_c 0.000 | brownian_eta 0.161 | 35968.55832407983
iter 108 | elbo -0.770 | kl 414.968 | loss 367.882 | |mu| 0.500 | sig 0.000 | scale 0.545 | ell 1.392 | lik_sig 0.552 | brownian_c 0.000 | brownian_eta 0.161 |
iter 135 | elbo -0.648 | kl 415.350 | loss 388.084 | |mu| 0.500 | sig 0.000 | scale 0.497 | ell 1.643 | lik_sig 0.454 | brownian_c 0.000 | brownian_eta 0.161 |
150 |mu| 0.500 | sig 0.000 | scale 0.474 | ell 1.780 | lik_sig 0.434 | brownian_c 0.000 | brownian_eta 0.161 | 39517.59616520833
iter 162 | elbo -0.587 | kl 414.338 | loss 398.698 | |mu| 0.500 | sig 0.000 | scale 0.460 | ell 1.876 | lik_sig 0.425 | brownian_c 0.000 | brownian_eta 0.161 |
iter 189 | elbo -0.563 | kl 415.042 | loss 406.132 | |mu| 0.500 | sig 0.000 | scale 0.435 | ell 2.046 | lik_sig 0.412 | brownian_c 0.000 | brownian_eta 0.161 |
iter 216 | elbo -0.551 | kl 414.446 | loss 409.485 | |mu| 0.500 | sig 0.000 | scale 0.418 | ell 2.169 | lik_sig 0.407 | brownian_c 0.000 | brownian_eta 0.161 |
iter 243 | elbo -0.545 | kl 414.953 | loss 412.283 | |mu| 0.500 | sig 0.000 | scale 0.405 | ell 2.265 | lik_sig 0.404 | brownian_c 0.000 | brownian_eta 0.161 |
250 |mu| 0.500 | sig 0.000 | scale 0.402 | ell 2.286 | lik_sig 0.404 | brownian_c 0.000 | brownian_eta 0.161 | 41255.30519089216
iter 270 | elbo -0.542 | kl 414.170 | loss 412.841 | |mu| 0.500 | sig 0.000 | scale 0.395 | ell 2.343 | lik_sig 0.402 | brownian_c 0.000 | brownian_eta 0.161 |
iter 297 | elbo -0.539 | kl 414.172 | loss 413.621 | |mu| 0.500 | sig 0.000 | scale 0.387 | ell 2.409 | lik_sig 0.401 | brownian_c 0.000 | brownian_eta 0.161 |
iter 324 | elbo -0.537 | kl 414.605 | loss 414.506 | |mu| 0.500 | sig 0.000 | scale 0.380 | ell 2.467 | lik_sig 0.401 | brownian_c 0.000 | brownian_eta 0.161 |
350 |mu| 0.500 | sig 0.000 | scale 0.375 | ell 2.516 | lik_sig 0.400 | brownian_c 0.000 | brownian_eta 0.161 | 41519.8542502454
iter 351 | elbo -0.536 | kl 414.804 | loss 414.969 | |mu| 0.500 | sig 0.000 | scale 0.375 | ell 2.518 | lik_sig 0.400 | brownian_c 0.000 | brownian_eta 0.161 |
iter 378 | elbo -0.535 | kl 415.226 | loss 415.545 | |mu| 0.500 | sig 0.000 | scale 0.370 | ell 2.565 | lik_sig 0.400 | brownian_c 0.000 | brownian_eta 0.161 |
iter 405 | elbo -0.534 | kl 414.598 | loss 415.006 | |mu| 0.500 | sig 0.000 | scale 0.366 | ell 2.607 | lik_sig 0.400 | brownian_c 0.000 | brownian_eta 0.161 |
iter 432 | elbo -0.534 | kl 414.101 | loss 414.561 | |mu| 0.500 | sig 0.000 | scale 0.363 | ell 2.647 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 459 | elbo -0.533 | kl 415.375 | loss 415.865 | |mu| 0.500 | sig 0.000 | scale 0.360 | ell 2.684 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 486 | elbo -0.533 | kl 415.280 | loss 415.787 | |mu| 0.500 | sig 0.000 | scale 0.358 | ell 2.719 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
500 |mu| 0.500 | sig 0.000 | scale 0.357 | ell 2.736 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 | 41430.51063560744
iter 513 | elbo -0.532 | kl 414.655 | loss 415.173 | |mu| 0.500 | sig 0.000 | scale 0.356 | ell 2.752 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 540 | elbo -0.532 | kl 414.321 | loss 414.845 | |mu| 0.500 | sig 0.000 | scale 0.354 | ell 2.783 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 567 | elbo -0.532 | kl 414.058 | loss 414.585 | |mu| 0.500 | sig 0.000 | scale 0.353 | ell 2.813 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 594 | elbo -0.532 | kl 414.902 | loss 415.431 | |mu| 0.500 | sig 0.000 | scale 0.352 | ell 2.843 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 621 | elbo -0.531 | kl 415.630 | loss 416.160 | |mu| 0.500 | sig 0.000 | scale 0.352 | ell 2.871 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 648 | elbo -0.531 | kl 414.720 | loss 415.250 | |mu| 0.500 | sig 0.000 | scale 0.351 | ell 2.898 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 675 | elbo -0.531 | kl 414.549 | loss 415.079 | |mu| 0.500 | sig 0.000 | scale 0.351 | ell 2.924 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 702 | elbo -0.531 | kl 414.686 | loss 415.217 | |mu| 0.500 | sig 0.000 | scale 0.351 | ell 2.950 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 729 | elbo -0.531 | kl 414.893 | loss 415.424 | |mu| 0.500 | sig 0.000 | scale 0.351 | ell 2.975 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
750 |mu| 0.500 | sig 0.000 | scale 0.351 | ell 2.994 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 | 41595.048506881336
iter 756 | elbo -0.531 | kl 415.057 | loss 415.587 | |mu| 0.500 | sig 0.000 | scale 0.351 | ell 2.999 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 783 | elbo -0.531 | kl 414.525 | loss 415.056 | |mu| 0.500 | sig 0.000 | scale 0.351 | ell 3.023 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 810 | elbo -0.530 | kl 415.801 | loss 416.331 | |mu| 0.500 | sig 0.000 | scale 0.352 | ell 3.046 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 837 | elbo -0.530 | kl 414.696 | loss 415.226 | |mu| 0.500 | sig 0.000 | scale 0.352 | ell 3.069 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 864 | elbo -0.530 | kl 414.470 | loss 415.001 | |mu| 0.500 | sig 0.000 | scale 0.353 | ell 3.091 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 891 | elbo -0.530 | kl 413.926 | loss 414.457 | |mu| 0.500 | sig 0.000 | scale 0.354 | ell 3.114 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 918 | elbo -0.530 | kl 414.147 | loss 414.677 | |mu| 0.500 | sig 0.000 | scale 0.355 | ell 3.135 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 945 | elbo -0.530 | kl 414.429 | loss 414.959 | |mu| 0.500 | sig 0.000 | scale 0.356 | ell 3.157 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 972 | elbo -0.530 | kl 415.509 | loss 416.039 | |mu| 0.500 | sig 0.000 | scale 0.357 | ell 3.178 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 999 | elbo -0.530 | kl 414.016 | loss 414.546 | |mu| 0.500 | sig 0.000 | scale 0.358 | ell 3.199 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
1000 |mu| 0.500 | sig 0.000 | scale 0.358 | ell 3.199 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 | 41541.80924897452
iter 1026 | elbo -0.530 | kl 415.309 | loss 415.838 | |mu| 0.500 | sig 0.000 | scale 0.359 | ell 3.219 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1053 | elbo -0.530 | kl 415.001 | loss 415.530 | |mu| 0.500 | sig 0.000 | scale 0.360 | ell 3.239 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1080 | elbo -0.530 | kl 414.742 | loss 415.271 | |mu| 0.500 | sig 0.000 | scale 0.361 | ell 3.259 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1107 | elbo -0.530 | kl 414.342 | loss 414.871 | |mu| 0.500 | sig 0.000 | scale 0.362 | ell 3.279 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.162 |
iter 1134 | elbo -0.530 | kl 415.311 | loss 415.840 | |mu| 0.500 | sig 0.000 | scale 0.364 | ell 3.299 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1161 | elbo -0.530 | kl 414.179 | loss 414.708 | |mu| 0.500 | sig 0.000 | scale 0.365 | ell 3.319 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.162 |
iter 1188 | elbo -0.529 | kl 414.269 | loss 414.798 | |mu| 0.500 | sig 0.000 | scale 0.366 | ell 3.338 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.162 |
iter 1215 | elbo -0.529 | kl 413.826 | loss 414.355 | |mu| 0.500 | sig 0.000 | scale 0.368 | ell 3.357 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1242 | elbo -0.529 | kl 414.570 | loss 415.100 | |mu| 0.500 | sig 0.000 | scale 0.369 | ell 3.376 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
1250 |mu| 0.500 | sig 0.000 | scale 0.370 | ell 3.382 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 | 41523.67677075849
iter 1269 | elbo -0.529 | kl 414.489 | loss 415.019 | |mu| 0.500 | sig 0.000 | scale 0.371 | ell 3.395 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1296 | elbo -0.529 | kl 414.150 | loss 414.680 | |mu| 0.500 | sig 0.000 | scale 0.372 | ell 3.414 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.162 |
iter 1323 | elbo -0.529 | kl 414.219 | loss 414.748 | |mu| 0.500 | sig 0.000 | scale 0.374 | ell 3.432 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.162 |
iter 1350 | elbo -0.529 | kl 414.898 | loss 415.427 | |mu| 0.500 | sig 0.000 | scale 0.375 | ell 3.451 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1377 | elbo -0.529 | kl 414.898 | loss 415.427 | |mu| 0.500 | sig 0.000 | scale 0.377 | ell 3.469 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.162 |
iter 1404 | elbo -0.529 | kl 414.542 | loss 415.071 | |mu| 0.500 | sig 0.000 | scale 0.378 | ell 3.488 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.162 |
iter 1431 | elbo -0.529 | kl 415.669 | loss 416.198 | |mu| 0.500 | sig 0.000 | scale 0.380 | ell 3.506 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1458 | elbo -0.529 | kl 414.078 | loss 414.607 | |mu| 0.500 | sig 0.000 | scale 0.381 | ell 3.524 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.162 |
iter 1485 | elbo -0.529 | kl 414.864 | loss 415.393 | |mu| 0.500 | sig 0.000 | scale 0.383 | ell 3.542 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
1500 |mu| 0.500 | sig 0.000 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 | 41478.34204845449
For inference, we again initialize from a linear model - this time a linear model prediction orientations in quaternion space.
[20]:
## first fit a linear model (we will use this for initialization and comparison) ##
Y2 = Y[..., n_ts1:] #test data
Z1, Z2 = qs_t[:n_ts1, :], qs_t[n_ts1:, :] #train/test quaternions
print(Y1.shape, Z1.shape)
alphas = 10**(np.linspace(-4, 4, 51)) #possible regularization strengths
clf = RidgeCV(alphas=alphas).fit(Y1[0, ...].T, Z1) #crossvalidated ridge regression
Z2_pred = clf.predict(Y2[0, ...].T) #predict test data
Z2_pred = Z2_pred / np.sqrt(np.sum(Z2_pred**2, axis = 1, keepdims = True)) #normalize
Z2_pred = np.sign(Z2_pred[:, :1]) * Z2_pred
errs_lin = 4*( 1 - np.sum(Z2 * Z2_pred, axis = 1)**2 )
errs_baseline = 4*( 1 - np.sum(np.array([1,0,0,0])[None, :] * Z2, axis = 1)**2 )
errs_baseline = deltas.flatten()
print('linear error:', np.quantile(errs_lin, [0.1, 0.25, 0.5, 0.75, 0.9]))
print('baseline/constant:', np.quantile(errs_baseline, [0.1, 0.25, 0.5, 0.75, 0.9]))
(1, 100, 400) (400, 4)
linear error: [0.2881247 0.66655339 1.59165241 3.06419977 3.79916018]
baseline/constant: [1.40482737 2.39040575 3.34394689 3.84129081 3.97570362]
This sets us up to construct our inference model.
[21]:
### now we want to do decoding ###
_, _, n_ts2 = Y2.shape
manif2 = mgp.manifolds.So3(n_ts2, d_latent) # latent manifold is still So(3)
mu2 = Z2_pred[None, ...] #initialize from linear prediction
lat_dist2 = mgp.rdist.ReLie(manif2, n_ts2, n_trials, sigma = 0.4, diagonal = False, mu = mu2) #variational distribution
#in this case we do not define a new prior
[22]:
#@title Construct SO(3) model
data2 = torch.Tensor(Y2).to(device) #put data on device
mod2 = mgp.models.SvgpLvm(n_neurons, n_ts2, n_trials, z.cpu(), kernel.cpu(), likelihood.cpu(), lat_dist2, lprior.cpu()).to(device) #use old generative model and new variational distribution
for p in mod2.parameters(): #no gradients for generative parameters
p.requires_grad = False
for p in mod2.lat_dist.parameters(): #only inference
p.requires_grad = True
#copy over tuning curves (this summarizes p(Y*|Z*, {Y, Z}) from the training data in the SVGP framework)
mod2.svgp.q_mu[...] = mod.svgp.q_mu[...].detach()
mod2.svgp.q_sqrt[...] = mod.svgp.q_sqrt[...].detach()
Finally we are ready to do inference!
[23]:
t0 = time.time()
# helper function to specify training parameters. We now do not mask the gradients.
train_params2 = mgp.crossval.training_params(max_steps = max_steps, n_mc = 30, lrate = 2.5e-2, print_every = 10, callback = cb_so3, burnin = 1, mask_Ts = (lambda x: x*1))
print('fitting', n_neurons, 'neurons and', n_ts2, 'time bins for', max_steps, 'iterations')
mod_train2 = mgp.crossval.train_model(mod2, data2, train_params2) #inference!
fitting 100 neurons and 400 time bins for 1501 iterations
iter 0 | elbo -0.623 | kl 0.018 | loss 0.623 | |mu| 0.500 | sig 0.400 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
0 |mu| 0.500 | sig 0.400 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 | 62.2546900889882
iter 10 | elbo -0.599 | kl 0.018 | loss 0.617 | |mu| 0.500 | sig 0.336 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 20 | elbo -0.584 | kl 0.020 | loss 0.603 | |mu| 0.500 | sig 0.273 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 30 | elbo -0.574 | kl 0.021 | loss 0.595 | |mu| 0.500 | sig 0.230 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 40 | elbo -0.568 | kl 0.023 | loss 0.591 | |mu| 0.500 | sig 0.202 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 50 | elbo -0.564 | kl 0.024 | loss 0.588 | |mu| 0.500 | sig 0.185 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
50 |mu| 0.500 | sig 0.185 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 | 58.83990364661772
iter 60 | elbo -0.562 | kl 0.025 | loss 0.587 | |mu| 0.500 | sig 0.175 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 70 | elbo -0.561 | kl 0.025 | loss 0.586 | |mu| 0.500 | sig 0.170 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 80 | elbo -0.560 | kl 0.026 | loss 0.586 | |mu| 0.500 | sig 0.168 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 90 | elbo -0.560 | kl 0.026 | loss 0.585 | |mu| 0.500 | sig 0.168 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 100 | elbo -0.559 | kl 0.026 | loss 0.585 | |mu| 0.500 | sig 0.168 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
100 |mu| 0.500 | sig 0.168 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 | 58.49902128107196
iter 110 | elbo -0.559 | kl 0.026 | loss 0.585 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 120 | elbo -0.559 | kl 0.026 | loss 0.585 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 130 | elbo -0.559 | kl 0.026 | loss 0.585 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 140 | elbo -0.559 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 150 | elbo -0.559 | kl 0.026 | loss 0.585 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
150 |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 | 58.45806742648572
iter 160 | elbo -0.559 | kl 0.026 | loss 0.585 | |mu| 0.500 | sig 0.168 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 170 | elbo -0.558 | kl 0.026 | loss 0.585 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 180 | elbo -0.559 | kl 0.026 | loss 0.585 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 190 | elbo -0.559 | kl 0.026 | loss 0.585 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 200 | elbo -0.559 | kl 0.026 | loss 0.585 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 210 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 220 | elbo -0.559 | kl 0.026 | loss 0.585 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 230 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 240 | elbo -0.559 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 250 | elbo -0.559 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
250 |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 | 58.41505519923592
iter 260 | elbo -0.559 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 270 | elbo -0.559 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.168 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 280 | elbo -0.559 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.168 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 290 | elbo -0.559 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 300 | elbo -0.559 | kl 0.026 | loss 0.585 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 310 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 320 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 330 | elbo -0.559 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 340 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 350 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
350 |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 | 58.4201060165533
iter 360 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.168 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 370 | elbo -0.559 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 380 | elbo -0.559 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 390 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 400 | elbo -0.559 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 410 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 420 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 430 | elbo -0.559 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 440 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.168 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 450 | elbo -0.559 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 460 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 470 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 480 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.168 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 490 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 500 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.168 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
500 |mu| 0.500 | sig 0.168 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 | 58.41072910788002
iter 510 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.168 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 520 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 530 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 540 | elbo -0.559 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 550 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 560 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 570 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 580 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 590 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 600 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 610 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 620 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 630 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 640 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 650 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 660 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 670 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 680 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 690 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 700 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 710 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 720 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 730 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 740 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 750 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
750 |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 | 58.39515554302095
iter 760 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 770 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 780 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 790 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 800 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.168 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 810 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 820 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 830 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 840 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 850 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 860 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 870 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 880 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 890 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 900 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 910 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 920 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 930 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 940 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 950 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 960 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 970 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 980 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 990 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1000 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
1000 |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 | 58.38274132637594
iter 1010 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1020 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1030 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1040 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1050 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1060 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1070 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1080 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1090 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1100 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1110 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1120 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1130 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1140 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1150 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1160 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.168 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1170 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1180 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1190 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1200 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1210 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1220 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1230 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1240 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1250 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
1250 |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 | 58.36953732996062
iter 1260 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1270 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1280 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1290 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1300 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1310 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1320 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1330 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1340 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1350 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1360 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1370 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1380 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1390 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1400 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1410 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1420 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1430 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1440 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1450 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1460 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1470 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1480 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.166 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1490 | elbo -0.558 | kl 0.026 | loss 0.584 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
iter 1500 | elbo -0.558 | kl 0.026 | loss 0.583 | |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 |
1500 |mu| 0.500 | sig 0.167 | scale 0.384 | ell 3.552 | lik_sig 0.399 | brownian_c 0.000 | brownian_eta 0.161 | 58.34791888432438
After performing inference, we compare our model to the linear and constant baselines and see that it vastly outperforms them.
[24]:
Z2_mgplvm = mod2.lat_dist.prms[0].detach().cpu().numpy()[0, ...] #mgplvm prediction
print(Z2_mgplvm.shape)
errs_mgplvm = 4*( 1 - np.sum(Z2 * Z2_mgplvm, axis = 1)**2 )
cols = ['g', 'b', 'k']
bins = np.linspace(0, np.pi, 11)
#bins = np.linspace(0, np.pi**2, 11)
plt.figure()
labels = ['constant', 'linear', 'mgplvm']
for idat, dat in enumerate([errs_baseline, errs_lin, errs_mgplvm]):
dat = np.arccos( 1 - 0.5*dat)
#dat = dat**2
plt.hist(dat, bins = bins, alpha = 0.3, color = cols[idat], density = True,
histtype = ('step' if idat == 0 else 'bar'), lw = 5, label = labels[idat])
plt.axvline(np.mean(dat), color = cols[idat], lw = 4)
print(labels[idat]+' mean error:', np.mean(dat))
plt.xlabel('geodesic error')
plt.ylabel('frequency')
plt.yticks([])
plt.xticks([0, np.pi/2, np.pi], [r'$0$', r'$\pi / 2$', r'$\pi$'])
plt.legend(frameon = False, loc = 'upper center', bbox_to_anchor = (0.5, 1.2), ncol = 3, fontsize = 16)
plt.show()
print('total time for SO(3):', time.time() - tic)
(400, 4)
constant mean error: 2.206467350300819
linear mean error: 1.4969529603467293
mgplvm mean error: 0.6597242035160659
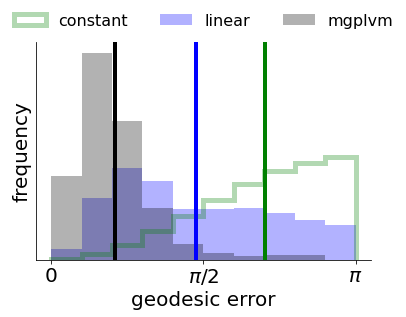
total time for SO(3): 180.98119020462036
The rest is legacy code that I used for debugging
[25]:
# print(Y1 == Y2)
# print(thetas[:n_ts1] == thetas2)
# print(mod2, mod)
# print('\nkernel ell')
# print(mod.svgp.kernel.ell)
# print(mod2.svgp.kernel.ell)
# print('\nkernel scale')
# print(mod.svgp.kernel.scale_sqr)
# print(mod2.svgp.kernel.scale_sqr)
# print('\nlikelihood prms')
# print(mod.svgp.likelihood.prms)
# print(mod2.svgp.likelihood.prms)
# print('\ninducing points')
# print(mod.svgp.z.z[:3, 0, 0])
# print(mod2.svgp.z.z[:3, 0, 0])
# print('\nlat mu')
# print(mod.lat_dist.lat_prms()[0][0, :10, 0])
# print(mod2.lat_dist.lat_prms()[0][0, :10, 0])
# print('\nlat std')
# print(mod.lat_dist.lat_prms()[1][0, :10, 0])
# print(mod2.lat_dist.lat_prms()[1][0, :10, 0])
# print('\nqmu')
# print(mod.svgp.q_mu.requires_grad)
# print(mod2.svgp.q_mu.requires_grad)
# print(mod(data1, 10))
# print(mod2(data2, 10))
# print(len([p for p in mod.parameters()]))
# for p in mod2.parameters():
# print(p.requires_grad)